5 Variable K Map Ppt

5 variable k map ppt

Now we have two squares and we can loop octets quads and pairs between these two squares. 5 variable k map use two 4 variable map to form a 5 variable k map 16 16 32 a b c d e a in the bottom layer a in the top layer.

Digital Circuits K Map Method Tutorialspoint

Let the 5 variable boolean function be represented as.

Karnaugh maps k maps if m i is a minterm of f then place a 1 in cell i of the k map. If you have 5 variables you ll need 2 k map let s say the variables are a b c d and e. F p q r s t where p q r s t are the variables and p is the most significant bit variable and t is the least significant bit variable. How many k map is needed.

K map cells are arranged such that adjacent cells correspond to truth rows that differ in only one bit position logical adjacency. If d i is a don. Karnaugh maps k maps an n variable k map has 2n cells with each cell corresponding to an n variable truth table value. Any boolean expression or function comprising of 5 variables can be solved using the 5 variable k map.

I e grouping of min terms from m 0 to m 15 and m 16 to m 31. Now we can easily see which minterms contain common literals. K map is table like representation but it gives more information than truth table. To five variable plot it on a karnaugh map.

We can minimize boolean expressions of 3 4 variables very easily using k map without using any boolean algebra theorems. Minterms on the left and right sides contain y and y respectively. We fill grid of k map with 0 s and 1 s then solve it by making groups. K map cells are labeled with the corresponding truth table row.

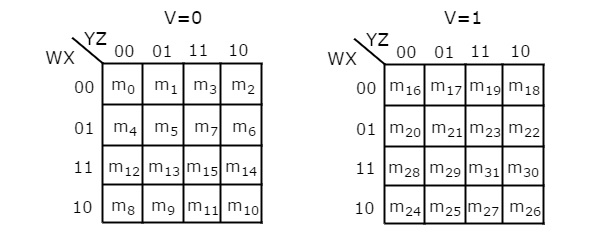
We can re arrange these minterms into a karnaugh map. There are two possibilities of grouping 16 adjacent min terms. A 5 variable boolean function can have a maximum of 32 minterms. A 5 variable k map is drawn as below.

The number of cells in 5 variable k map is thirty two since the number of variables is 5. Chap 5 c h 29. X y minterm 0 0 x y 0 1 x y 1 0 xy 1 1 xy y 0 1 0 x y x y x 1 xy xy 5 6. It is represented by f a b c d e.

K map for two variables a two variable function has four possible minterms. The function may be given in minterm maxterm or algebraic form. There is only one possibility of grouping 32 adjacent min terms. Minterms in the top and bottom rows contain x and x respectively y 0 1 0 x y x y x 1 xy xy y y x x y x.

If m i is a maxterm of f then place a 0 in cell i. The following figure shows 5 variable k map. K map can take two forms sum of product sop and product of sum pos according to the need of problem. Again as we did with 3 variable 4 variable k map carefully note the numbering of each cell.

What we need to do is to visualize second square on first square and figure out adjacent cells. Such a 5 variable k map must contain 32 cells. All the possible minterms are represented below in 5 variable k map we have 32 cells as shown below.

All the possible minterms are represented below in 5 variable k map we have 32 cells as shown below. Such a 5 variable k map must contain 32 cells. What we need to do is to visualize second square on first square and figure out adjacent cells.

usc upstate campus map us times zones map

Karnaugh Maps K Map 1 6 Variables Simplification Examples

Karnaugh Maps K Map 1 6 Variables Simplification Examples

5 Variable K Map Youtube

Karnaugh Maps K Map 1 6 Variables Simplification Examples